Technology Sharing

한어Русский языкEnglishFrançaisIndonesianSanskrit日本語DeutschPortuguêsΕλληνικάespañolItalianoSuomalainenLatina

week46 FMP

Summary

This week I read a paper titled Chasing Fairness in Graphs: A GNN Architecture Perspective. This paper proposes a fair message passing scheme (FMP) guided by a unified optimization framework for graph neural networks (GNNs), which aims to improve the fairness of graph data processing. The scheme is implemented through two core steps: first, aggregating graph data, and then explicitly pursuing representations of the centers of various statistical groups to reduce bias. The method constructs an optimization problem that considers both fairness and data smoothness, and uses Fenchel conjugation and gradient descent techniques combined with the characteristics of the softmax function to efficiently solve it and generate node representations that are both fair and informative. This scheme is directly embedded in GNNs to improve the fairness and accuracy of node classification tasks without the need for data preprocessing. Experimental results show that on real datasets, FMP performs better than multiple baseline models, and its effectiveness is fully verified from the perspectives of model architecture, efficiency, and sensitive attribute utilization.

Abstract

This week’s weekly newspaper decodes the paper entitled Chasing Fairness in Graphs: A GNN Architecture Perspective. This paper introduces a Fair Message Passing (FMP) scheme guided by a unified optimization framework of Graph Neural Networks (GNNs), aiming to enhance fairness in graph data processing. The FMP achieves this through two core steps: first, aggregating graph data, and then explicitly striving to represent the centers of various statistical groups to mitigate bias. This approach formulates an optimization problem that considers both fairness and data smoothness, and leverages Fenchel duality and gradient descent techniques, combined with the properties of the softmax function, to efficiently solve the problem and generate fair and informative node representations. This scheme is directly embedded into GNNs to improve the fairness and accuracy of node classification tasks, without the need for data preprocessing. Experimental results on real-world datasets show that FMP outperforms multiple baseline models, comprehensively validating its effectiveness from the perspectives of model architecture, efficiency, and the utilization of sensitive attributes.

1. Title

标题：Chasing Fairness in Graphs: A GNN Architecture Perspective

作者：Zhimeng Jiang1, Xiaotian Han1, Chao Fan2, Zirui Liu3, Na Zou4, Ali Mostafavi1, Xia Hu3

release:Vol. 38 No. 19: AAAI-24

Link: https://doi.org/10.1609/aaai.v38i19.30115

2. Abstract

This paper aims to achieve better fairness through a new GNN framework, so it proposes a unified optimization framework designed within the GNNFair Message Passing (FMP)It is worth noting that FMP usesCross Entropy LossExplicitly present the use of sensitive attributes in the forward propagation of node classification tasks, whileNo data preprocessing requiredIn FMP, firstly adoptpolymerizationto use the neighbor's information, and thenBias MitigationThe step explicitly pushes the data statistics group node representation centers together. In this way, the FMP scheme can aggregate useful information from neighbors and alleviate bias to achieve better fairness and prediction trade-off performance.Node ClassificationExperiments on the task show that the proposed FMP outperforms multiple baselines in terms of fairness and accuracy on three real-world datasets.

3. FMP

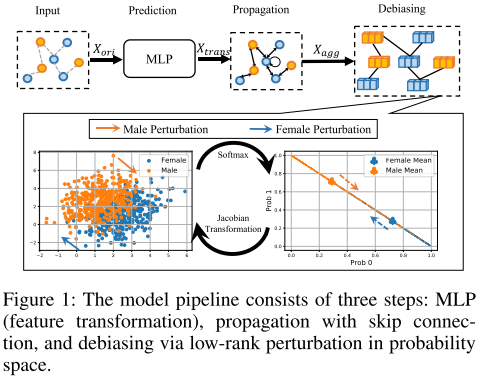
FMP can achieve fair prediction from the perspective of the model backbone. Specifically, fair message passing is formulated as an optimization problem to pursue smoothness and fair node representation simultaneously. Combined with an effective and efficient optimization algorithm, a closed-form fair message passing is derived. Finally, the proposed FMP is integrated into a fair GNN in three stages, including transformation, aggregation, and debiasing steps, as shown in Figure 1. These three stages adopt node features, graph topology, and sensitive attributes, respectively.

3.1 Optimization Framework

$$\underset{\mathbf{F}}{\min }\frac{{\lambda }_s}{2}tr({\mathbf{F}}^T\tilde{\mathbf{T}}\mathbf{F})\frac{1}{2}||\mathbf{F}-{\mathbf{X}}_{trans}|{|}_F^2{\lambda }_f||{\Delta }_{s}SF(\mathbf{F})|{|}_1\text{\hspace{1em}(1)}$$

$tilde L $represents\; the\; normalized\; Laplacian\; matrix,$h_s(·)$ and $h_f(\cdot )$ represents the smoothness and fairness objectives,$X_{trans}\in R^{n\times d_{out}}$ is the transformed$d_{out}$Dimension node features.$F\in R^{n\times d_{out}}$​ are aggregated node features of the same matrix size.

The first two terms preserve the similarity of connected node representations, thereby enhancing the smoothness of the graph. The last term enforces fair node representations so that the average predicted probability between different sensitive attribute groups can remain unchanged.

The regularization coefficients λs and λf adaptively control the trade-off between graph smoothness and fairness.
$$h_s(\mathbf{F})=\underset{\mathbf{F}}{\min }\frac{{\lambda }_s}{2}tr({\mathbf{F}}^T\tilde{\mathbf{T}}\mathbf{F})\frac{1}{2}||\mathbf{F}-{\mathbf{X}}_{trans}|{|}_F^2$$
Smoothness objective hs(·): The adjacency matrix in existing graph message passing schemes is normalized to improve numerical stability and achieve superior performance. From an edge-centric perspective, the smoothness objective enforces that the connected nodes are represented similarly, since
$$tr({\mathbf{F}}^T\tilde{\mathbf{T}}\mathbf{F})=\sum _{(v_i,v_j)\in \mathrm{E}}||\frac{{\mathbf{F}}_i}{\sqrt{d_{i}1}}-\frac{{\mathbf{F}}_i}{\sqrt{d_{j}1}}|{|}_F^2\text{\hspace{1em}(2)}$$
Fairness target hf(·): The fairness target measures the deviation of the node representation after aggregation. The sensitive attribute event vector Δs represents the sensitive attribute group and group size by summing the sign and absolute value. The sensitive attribute event vector is
Δ s = 1