Technology Sharing

한어Русский языкEnglishFrançaisIndonesianSanskrit日本語DeutschPortuguêsΕλληνικάespañolItalianoSuomalainenLatina

PDF document public account reply keyword: 20240711

2020 CSP-J Multiple Choice Questions

Multiple-choice questions (15 questions in total, 2 points each, 30 points in total: each question has only one correct answer)

10. There are 5 children standing side by side in a row, two of them are twins. If the two twins must be adjacent to each other, how many different ways are there to arrange them?

A.48

B.36

C.24

D.72

13. The Chinese calendar is a traditional way of recording years, which consists of 10 heavenly stems and 12 earthly branches, forming 60 heavenly stems and earthly branches. The corresponding heavenly stems and earthly branches can be converted from the Gregorian calendar year using the following formula and table.
Heavenly Stems = (Gregorian calendar year) divided by 10
Earthly Branch = remainder of (Gregorian calendar year) divided by 12

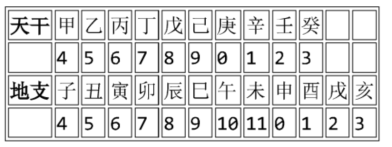
For example, this year is 2020. When 2020 is divided by 10, the remainder is 0, which is "Geng" in the table; when 2020 is divided by 12, the remainder is 4, which is "Zi" in the table, so this year is the Gengzi year.
What is the Heavenly Stems and Earthly Branches of 1949?

A. Jiyou

B. Ji Hai

C.Jichou

D.Jimao

14. There are 10 three-good students assigned to 7 classes. Each class has at least one quota. There are a total of ( ) different allocation plans.

A.84

B.72

C.56

D.504

15. There are five pairs of gloves of different colors (a total of 10 gloves, 1 glove for each hand), and 6 gloves are taken at a time. How many different ways are there to make exactly two pairs of gloves?

A.120

B.180

C.150

D.30

2 Related knowledge points

1) Multiplication principle

To do something, you need to divide it into n steps. There are m1 different ways to do the first step, m2 different ways to do the second step, and so on. There are mn different ways to do the nth step.

Then there are N=m1 * m2 * m3 …* mn different ways to accomplish this task.

Each step does not complete one thing, but only completes one of the steps

For example

The clown in the circus has three hats: red, yellow, and blue, and two pairs of shoes: black and white. He wears a hat and a pair of shoes every time he performs. Question: How many different combinations of a clown's hat and shoes are there?

analyze

There are two steps to dressing before a performance

Step 1: Choose a hat. There are 3 ways to choose.

Step 2: Choose a pair of shoes. There are two ways to choose.

Divide into 2 steps to fit the multiplication principle, a total of 3 * 2 = 6 combinations

2) Bundling

The adjacency problem in permutations and combinations can be solved by bundling method.

The basic idea of ​​this method is to treat the elements that require adjacent elements as a whole (i.e. a "big element") and then arrange them together with other elements. At the same time, it is necessary to pay attention to the arrangement of the elements inside this "big element".

Specific steps are as follows:

Requires adjacent elements to be bundled together and treated as a whole.

Arrange this whole together with other elements.

Consider the arrangement of the elements within this whole. Since they are adjacent, you need to consider their relative order.

Example 1

5 boys and 3 girls are lined up in a row. The 3 girls must line up together. How many different ways are there to line them up? ( )

A. 240 B. 320 C. 450 D. 4320

Answer D

analyze

The three girls must be together, using the binding method, tying the three girls together as one element

step 1

Consider the three girls as one element and arrange them with the five boys. There are A(6,6)=6 * 5 * 4 * 3 *2 * 1=720.

Step 2

The 3 girls are arranged again, A(3,3) = 3 * 2 * 1=6

It takes 2 steps to complete. You need to use the multiplication principle to multiply the number of permutations in the 2 steps: 720 * 6 = 4320

2) Partition method

The problem of distributing n identical elements to m different objects, requiring that all elements are distributed and each object is assigned at least one element.

Insert m-1 boards into n-1 spaces between n elements to divide n elements into m groups.

There are C(n-1,m-1) species in total

n-1 means there are n-1 spaces between n elements, and m-1 means m-1 boards can be divided into m groups

example

There are 7 identical apples to be divided among 3 children, each of whom should get at least 1 apple. How many ways are there to divide them?

analyze

7 identical apples need to be divided among 3 children. That is, the 7 identical apples are divided into 3 groups. Two partitions are inserted into the 6 spaces formed by the 7 apples.

C(6,2)=6 * 5 /(2 * 1) = 15 types

Exclusion

When there are many eligible cases and only a few ineligible cases, it is appropriate to subtract the ineligible cases from all the cases.

example

How many different ways are there to choose 4 people from 6 boys and 5 girls to participate in a competition, requiring at least 1 boy and 1 girl?

A.240 B.310 C.720 D.1080

analyze

The opposite of at least one male and one female is to select only males or only females, so that it can be changed to C(11,4)-C(6,4)-C(5,4)=310

3 Thought Analysis

10. There are 5 children standing side by side in a row, two of them are twins. If the two twins must be adjacent to each other, how many (A) different ways are there to arrange them?

A.48

B.36

C.24

D.72

analyze

step 1

The twins must be adjacent to each other. To use the bundling method, you need to bundle the twins together as one and make permutations with the other three.

A(4,4)

Step 2

There is an order inside the twins, A is on the left, B is on the right or A is on the right and B is on the left

A(2,2)

According to the multiplication principle, A(4,4) * A(2,2) = 4 * 3 * 2 * 1 * 2 *1 = 48

13. The Chinese calendar is a traditional way of recording years, which consists of 10 heavenly stems and 12 earthly branches, forming 60 heavenly stems and earthly branches. The corresponding heavenly stems and earthly branches can be converted from the Gregorian calendar year using the following formula and table.
Heavenly Stems = (Gregorian calendar year) divided by 10
Earthly Branch = remainder of (Gregorian calendar year) divided by 12

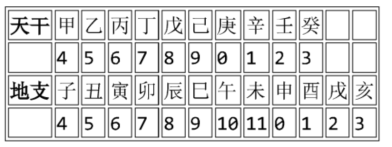
For example, this year is 2020. When 2020 is divided by 10, the remainder is 0, which is "Geng" in the table; when 2020 is divided by 12, the remainder is 4, which is "Zi" in the table, so this year is the Gengzi year.
What is the Heavenly Stems and Earthly Branches of 1949? (C)

A. Jiyou

B. Ji Hai

C.Jichou

D.Jimao

analyze

Heavenly Stems: 1949%10 = 9 corresponds to Ji

Earthly Branches: 1949%12 = 5 corresponds to Chou

So the 1949 year is Ji Chou.

14. There are 10 three-good students allocated to 7 classes. Each class has at least one quota. There are a total of (A) different allocation plans.

A.84

B.72

C.56

D.504

analyze

The same quota is divided into different classes. Each class has at least one quota. Use the partition method to divide into 7 classes and 7 groups, which requires 6 partitions.

6 partitions can be placed in 9 spaces

C(9,6)=C(9,3)=9 * 8 * 7 /(3 * 2 * 1) = 84

15. There are five pairs of gloves of different colors (a total of 10 gloves, 1 glove for each hand), and 6 gloves are taken at a time. How many different ways are there to make exactly two pairs of gloves?

A.120

B.180

C.150

D.30

analyze

step 1

Choose 2 pairs of gloves from 5 different colors

C(5,2)=5*4 /2=10

Step 2

You need to choose 6 gloves, but you still need 2 gloves. Choose 2 gloves from the remaining 6 gloves.

C(6,2)=6 * 5 /2 =15

Since 2 pairs of gloves have been selected in step 1, you cannot select only 1 pair in this step. Excluding the case of selecting only 1 pair, there are 3 situations in total.

15-3=12

According to the multiplication principle, 10 * 12 = 120