Technology Sharing

한어Русский языкEnglishFrançaisIndonesianSanskrit日本語DeutschPortuguêsΕλληνικάespañolItalianoSuomalainenLatina

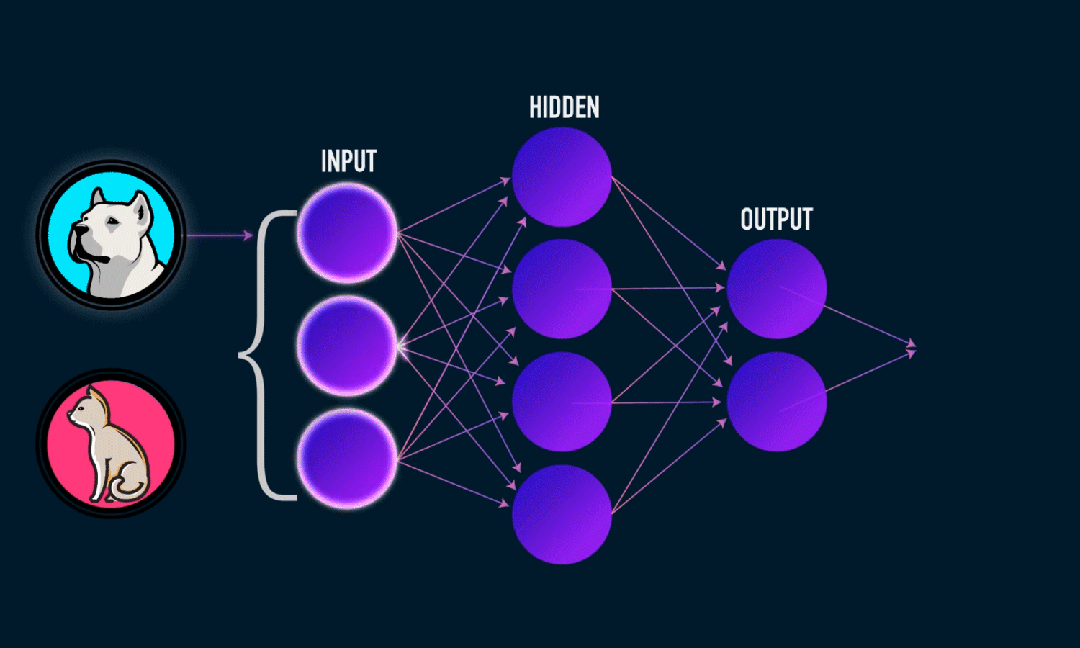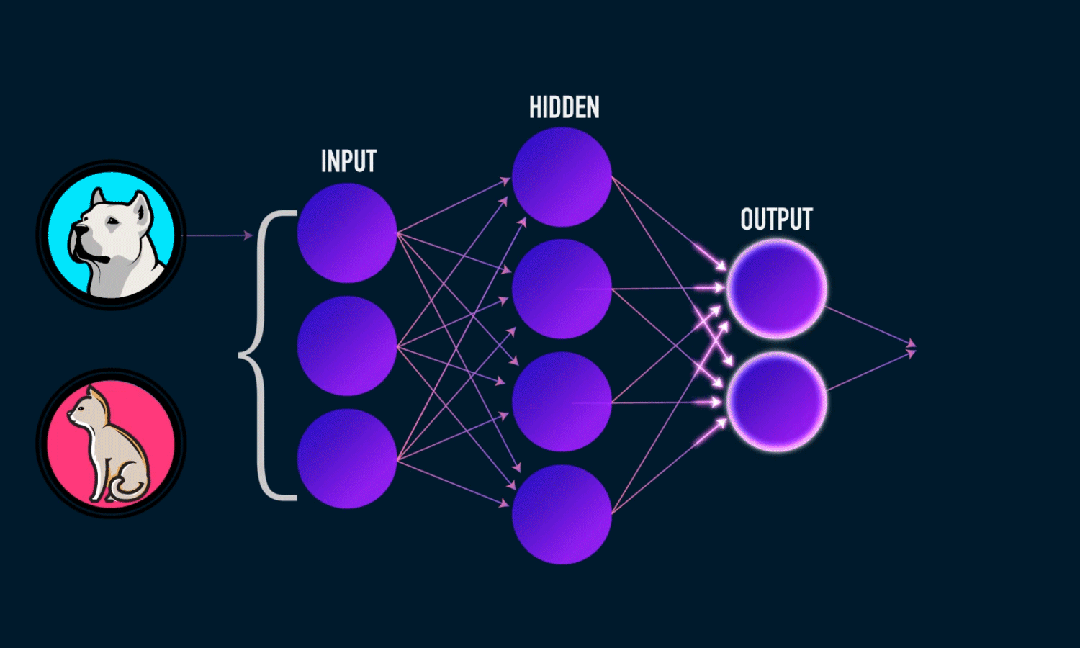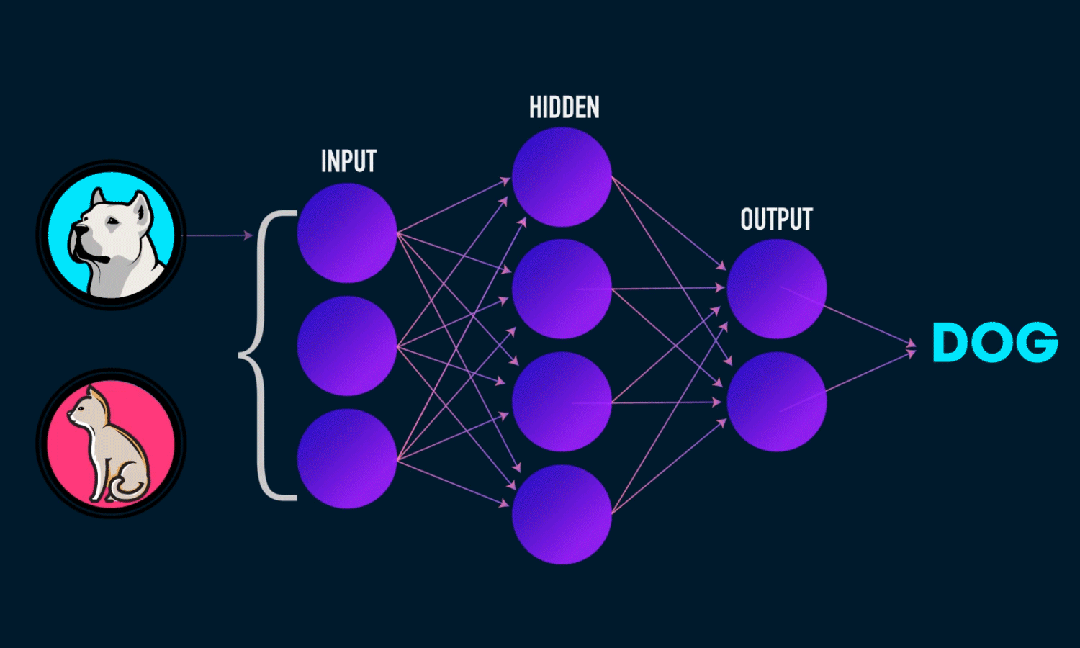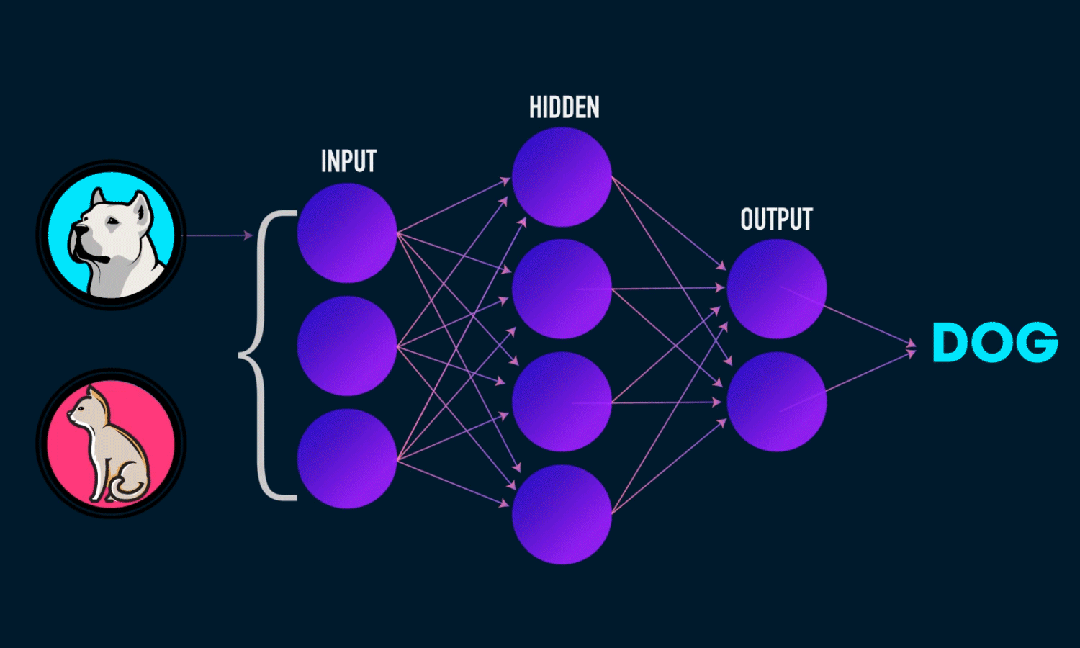
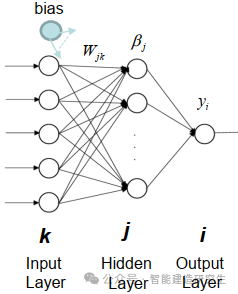
Extreme Learning Machine (ELM) is a simple single-layer feedforward neural network (SLFN) learning algorithm. In theory, the Extreme Learning Machine algorithm (ELM) tends to provide good performance at an extremely fast learning speed (a machine learning algorithm), which was proposed by Huang et al. The main feature of ELM is that it learns very quickly. Compared with traditional gradient descent methods (such as BP neural networks), ELM does not require an iterative process. Its basic principle is to randomly select the weights and biases of the hidden layer, and then learn the output weights by minimizing the error of the output layer.

img

The main steps of the ELM algorithm

1. Randomly initialize the weights and biases input to the hidden layer：

   • The weights and biases of the hidden layers are randomly generated and remain constant during training.

2. Calculate the output matrix of the hidden layer (that is, the output of the activation function)：

   • Use activation functions (such as sigmoid, ReLU, etc.) to calculate the output of the hidden layer.

3. Calculate output weights：

   • The weights from the hidden layer to the output layer are calculated using the least squares method.

The mathematical formula of ELM is as follows:

• Given a training data set , where ,

• The calculation formula of the output matrix of the hidden layer is:

  • Among them, is the input matrix, is the weight matrix input to the hidden layer, is the bias vector, and is the activation function.

• The calculation formula for the output weight is:

  • Where is the generalized inverse of the hidden layer output matrix and is the output matrix.

Application scenarios of ELM algorithm

1. Large-scale dataset processing：ELM performs well when processing large-scale data sets because it trains quickly and is suitable for scenarios that require fast model training, such as large-scale image classification, natural language processing and other tasks.

2. Industry Forecast：ELM has a wide range of applications in the field of industrial forecasting, such as quality control in industrial production processes, equipment failure prediction, etc. It can quickly train forecasting models and respond quickly to real-time data.

3. The financial sector：ELM can be used for financial data analysis and prediction, such as stock price prediction, risk management, credit scoring, etc. Since financial data is usually high-dimensional, ELM's fast training speed is very advantageous for processing such data.

4. Medical diagnosis: In the medical field, ELM can be used for tasks such as disease prediction and medical image analysis. It can quickly train models and classify or regress patient data to help doctors make faster and more accurate diagnoses.

5. Intelligent control system: ELM can be used in intelligent control systems, such as smart homes, intelligent transportation systems, etc. By learning the characteristics and laws of the environment, ELM can help the system make intelligent decisions and improve the efficiency and performance of the system.

Python implementation of ELM algorithm

We usemake_moonsThis is a toy dataset commonly used for machine learning and deep learning classification tasks. The points it generates are distributed in two intersecting half-moon shapes, which is very suitable for demonstrating the performance and decision boundaries of classification algorithms.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
from sklearn.neural_network import MLPClassifier
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import accuracy_score
 
# 定义极限学习机（ELM）类
class ELM:
    def __init__(self, n_hidden_units):
        # 初始化隐藏层神经元数量
        self.n_hidden_units = n_hidden_units
 
    def _sigmoid(self, x):
        # 定义Sigmoid激活函数
        return 1 / (1 + np.exp(-x))
 
    def fit(self, X, y):
        # 随机初始化输入权重
        self.input_weights = np.random.randn(X.shape[1], self.n_hidden_units)
        # 随机初始化偏置
        self.biases = np.random.randn(self.n_hidden_units)
        # 计算隐藏层输出矩阵H
        H = self._sigmoid(np.dot(X, self.input_weights) + self.biases)
        # 计算输出权重
        self.output_weights = np.dot(np.linalg.pinv(H), y)
 
    def predict(self, X):
        # 计算隐藏层输出矩阵H
        H = self._sigmoid(np.dot(X, self.input_weights) + self.biases)
        # 返回预测结果
        return np.dot(H, self.output_weights)
 
# 创建数据集并进行预处理
X, y = make_moons(n_samples=1000, noise=0.2, random_state=42)
# 将标签转换为二维数组（ELM需要二维数组作为标签）
y = y.reshape(-1, 1)
 
# 标准化数据
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
 
# 拆分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.3, random_state=42)
 
# 训练和比较ELM与MLP
 
# 训练ELM
elm = ELM(n_hidden_units=10)
elm.fit(X_train, y_train)
y_pred_elm = elm.predict(X_test)
# 将预测结果转换为类别标签
y_pred_elm_class = (y_pred_elm > 0.5).astype(int)
# 计算ELM的准确率
accuracy_elm = accuracy_score(y_test, y_pred_elm_class)
 
# 训练MLP
mlp = MLPClassifier(hidden_layer_sizes=(10,), max_iter=1000, random_state=42)
mlp.fit(X_train, y_train.ravel())
# 预测测试集结果
y_pred_mlp = mlp.predict(X_test)
# 计算MLP的准确率
accuracy_mlp = accuracy_score(y_test, y_pred_mlp)
 
# 打印ELM和MLP的准确率
print(f"ELM Accuracy: {accuracy_elm}")
print(f"MLP Accuracy: {accuracy_mlp}")
 
# 可视化结果
def plot_decision_boundary(model, X, y, ax, title):
    # 设置绘图范围
    x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
    y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
    # 创建网格
    xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.01),
                         np.arange(y_min, y_max, 0.01))
    # 预测网格中的所有点
    Z = model(np.c_[xx.ravel(), yy.ravel()])
    Z = (Z > 0.5).astype(int)
    Z = Z.reshape(xx.shape)
    # 画出决策边界
    ax.contourf(xx, yy, Z, alpha=0.8)
    # 画出数据点
    ax.scatter(X[:, 0], X[:, 1], c=y.ravel(), edgecolors='k', marker='o')
    ax.set_title(title)
 
# 创建图形
fig, axs = plt.subplots(1, 2, figsize=(12, 5))
 
# 画出ELM的决策边界
plot_decision_boundary(lambda x: elm.predict(x), X_test, y_test, axs[0], "ELM Decision Boundary")
# 画出MLP的决策边界
plot_decision_boundary(lambda x: mlp.predict(x), X_test, y_test, axs[1], "MLP Decision Boundary")
 
# 显示图形
plt.show()
 
# 输出：
'''
ELM Accuracy: 0.9666666666666667
MLP Accuracy: 0.9766666666666667
'''

Visualization output:

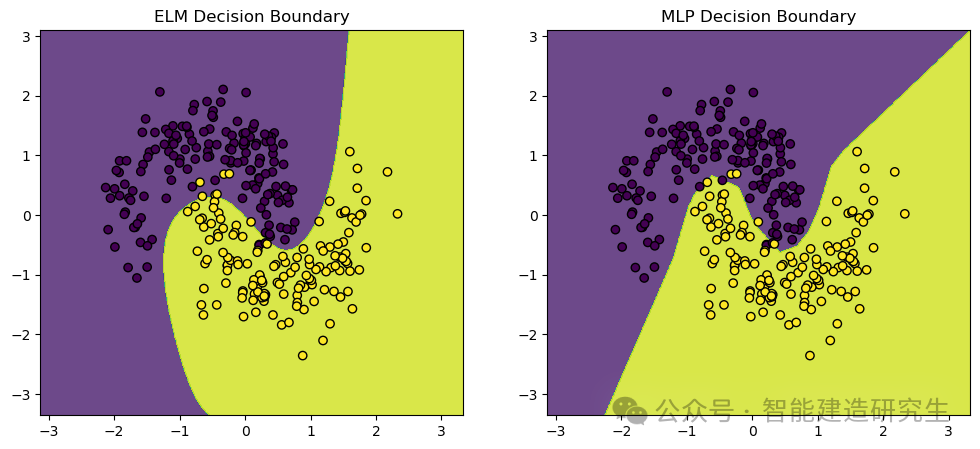
The above content is summarized from the Internet. If it is helpful, please forward it. See you next time!